THE NATIONAL LOTTERY

THE IN'S AND OUTS THE ODDS AND THE STATISTICS

WITHIN THESE PAGES WE HOPE GET THE FINGER OF FATE POINTING AT YOU

This page explains the statistics and how to work out the odds with graphic examples. If you have no interest in this you can skip to the next page. However I would suggest you print a hard copy to read at your leisure to give you a better understanding of how statistics within the National Lottery work, and why I suggest you concentrate on increasing your chances of getting a good return and not chasing the Jackpot prize only.

WITH THANKS TO:

While researching this site I read quite a few books, and visited many websites and web forums. Although trained as an accountant, I was still unaware of how the statistics and odds actually computed. We can be shown the actual odds and information, on many sites but it is my view that unless we know how to achieve them, we cannot not fully understand them, or the effect (or lack) upon our participating. I therefore offer my thanks to all those who have contributed in helping me understand the combinations and comprehend the formula's involved, especially those at the PC Advisor forum.

LENNY LOGO
It may be a little naïve of me to use the lottery logo but I have had many conversations with people at both the Home Office and Camelot the organisers of the UK National Lottery and none of them seem to wish to admit possession or allow restrictions on the copyright. It could be said that I am promoting their logo but If they ever decide, the ownership and restrictions I will remove said logo immediately, unless of course they do decide it is doing no harm and allow me to continue using it ..

Lottery the odds:
For some time I have being trying to study the odds of winning the UK National Lottery pick any six numbers from forty-nine
There are plenty of sites on the internet that explain the odds but most of those that I have come across although explain and give examples, use all forms of mathematic equations, notations, combinatorics, anyone with a degree in maths will understand these perfectly well, but those of use with no knowledge in these, find it just a little harder to comprehend.
This is my attempt to explain the combinatorics in plain English using the times (X) and divide (÷) symbols

To start lets do a simple sum to show the equation. Lets say we have picked a horse in each of six races on the card. And we want to place a bet which covers all the combinations of doubles and trebles. The first thing we need to know is how many doubles. i.e. how many 2's from 6 selections. For the first selection the odds are we need I from 6 for the second selection assuming we have the first we need the second from 5 remaining selections to get a double.We write this down as 1 x 2 divided by 6 x 5 = 2 divided by 30 = 15
Therefore there are a combination of 15 doubles from six selections.
To see how many doubles we have if one of our selections loses it is just a case of adjusting the equations and saying we have any 2 from 5 i.e. 1 x 2 divided by 5 x 4 = 2 ÷ 20 = 10. That is 1 from 5 and 2 (the second) from the 4 remaining races. Similarly if two horses lose the equation is adjusted so we have the 1 from 4 and the second to achieve a double from the remaining 3 races. Hence 1 x 2 ÷ 4 x 3 = 6 doubles. Therefore if all 6 selections win you have 15 doubles if 5 win 10 doubles if 4 win 6 doubles 3 win you have just 3 doubles and of course just 2 win you have only the one double.
The trebles are worked out exactly the same way. Assuming you get the first correct 1 from 6 (the second) 2 from 5 and (the third) 3 from 4 remaining races. i.e. 1x 2x 3 ÷ 6x 5x 4 = 6 ÷ 120 or 1 over 20 = 20 trebles. Again we can use the same equation to see how many trebles we have assuming one of our selections loses, we have 1 from 5 x 2 from 4 x 3 from 3, which is 1 x 2 x 3 ÷ 5 x 4 x 3 = 60 ÷ 6 = 10 trebles or if two lose 1 x 2 x 3 ÷ 4 x 3 x 2 = 4 (if you write down as 1 x 2 x 3 over 4 x 3 x 2 you would cancel the 2 x 3 to leave 1 over 4 avoiding the long multiplication and divisions) See example ;

NOW THE NATIONAL LOTTERY

This requires us to pick any 6 numbers from a possible 49. The order in which the numbers are picked is not important; you just have to pick the six numbers. The same applies for this as does the equation for 2 from 6 or 3 from 6 . i.e. If you attempt to select just one number from 49 lottery balls then the probability that you correctly predict are 1 in 49, therefore if you choose six numbers then the probability that one of your numbers is the same as the first ball drawn is 6 in 49. Given that the first number is chosen correctly, then the probability of drawing the second number correctly is 5 in 48. (i.e. there are 48 balls left in the drums and having correctly drawn the first number we have 5 selections left) Given we have the first two numbers the probability of getting a third is 4 in 47 and so on. 3 in 46, 2 in 45, and 1 in 44. So we write the equation out in just the same way: 1 x 2 x 3 x 4 x 5 x 6 (6 selections) over 49 x 48 x 47 x 46 x 45 x 44. After cancelling out cross multiplications we have the result. The odds of picking all six balls correctly are 1 in 13,983,816. See the example:-

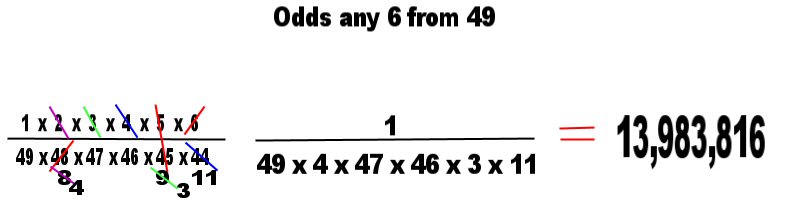
For the UK lottery we have a chance at the second prize by selecting and additional ball drawn this being the bonus number. What are the odds of selecting this number? Well there are 6 combinations of selecting 5 numbers (any 5 from 6 using our equation) and we have one chance of selecting the extra number, so our chances become 6 x 1 = 6 so assuming we already have 5 correct the odds of the 7th ball drawn being one of our selections is 13,983,816 ÷ 6 which gives us odds of 1 in 2,330,636.
How do we calculate the odds of getting the lower prizes? Well we know the odds for getting 6 from 49 that's 13,983,816. There are 6 winning numbers so there are 6 ways to select 1 out of 6. We know there are 43 numbers that don't win and using our equation we can determine that there are 962,596 ways to select 5 out of 43 numbers that don't win. We can then multiply by 6 and determine that there are 5,775,588 ways to select 6 from 49 with one that is a winning selection, divide this by the odds of (6_49) (i.e. 13,983,816) and we have odds of 0.41301945 or 2.42 to one.
Similarly the odds to select two correct are therefore (2_6) x (4_43) ÷ (6_49) which equals 1,851,150 ÷ 13,983,816 = 0.13237802 or 1 in 7.5
Three winning numbers are (3_6) x (3_43) ÷ (6_49) which equals 246,820 ÷ 13,983,816 = 0.01765040 or 1 in 57
Four winning numbers are (4_6) x (2_43) ÷ (6_49) = 13,545 ÷ 13,983,816 = 0.00096819 or 1 in 1,033
Five winning numbers are (5_6) x (1_43) ÷ (6_49) = 258 ÷ 13,983,816 = 0.00001844989 or 1 in 54,201

Euro Millions.
The lottery organisers make no secret of the odds of winning, in fact I think that under the law they are obliged to publish the odds. Winning the Euro millions jackpot is a staggering 76 million to one, they don't publish how they arrive at the figure but the calculation is easy to explain using our above formula.
The game requires we select 5 number from 50 and then select a further 2 balls from 9 star balls from another machine so we have a formula:- (5_50) x (2_9) which is exactly the same as saying (1 x 2 x 3 x 4 x 5 ÷ 50 x 49 x 48 x 47 x 46) x (1 x 2 ÷ 9 x 8) = 2,118,760 x 36 = 76,275,360. This is a popular formula for many of the big super State Lotteries in the United States, however they tend to use pick 5 from 50 and then just one star ball from 36, from the second machine. As you can see, the odds for the second machine are the same, as to select any 2 from 9 (2_9) is 36 to 1.

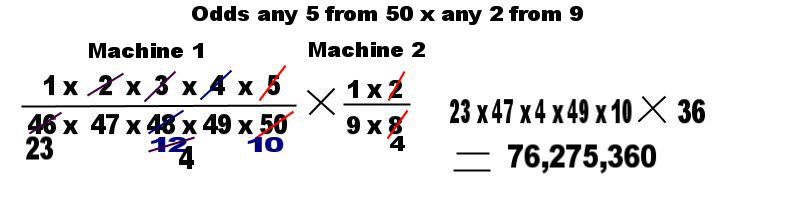
So for Euro Millions we have 2 machines and 2 formula to multiply to find the odds. i.e for lower prizes we have to calculate the odds of getting 1,2,3,4,or 5 correct and then multiply these odds by the probability of getting either 1 or 2 from the second machine. Working out the odds for 4 from the 50 is the same as explained for the National Lottery and then we just multiply by the second machine.
The probability of getting just one Star Ball is explained by the probability of getting the first is 2 from 9 = 36 to 1, assuming we do not have the first ball then the odds of the second ball being drawn is equal to 7 in 8, there are now only 8 balls left and there are seven that we don't have. So the odds are 7 in 18 = 2.5714. That is to say that the probability of getting the first Star ball without the second is 7 in 36 and the probability of not getting the first Star ball but getting the second is also 7 in 36. So to find the probability that we get one of these occurrences we just add the individual probabilities = 7/36 + 7/36 = 7/18 therefore the odds of getting 5 from the first machine with just one from the second is (5_50) = 2,118,760 x 18 ÷ 7 which is 5,448,240 to 1. exactly as the organisers state. If we divide the jackpot odds 76,275,360 by this we note that your chances of getting just 1 Star ball is 14 times greater than hitting the jackpot, this shows the odds to be correct, if there are 36 possible ways of choosing any 2 balls from nine in any order without replacing them back in the drum, then 14 of these ways will satisfy our requirements of matching just one star ball.
So the chances of winning the jackpot in the National Lottery are extremely high, and if we look at the Euro Millions the odds are more than 5 times greater still, so what do we do. Does the odds against us winning mean that the best strategy is not to play at all? Well the optimal strategy is to play, if you do not play you will never win, you have zero chance, which is entirely different to having a small wager and having a non zero chance. As my dad used to say "you've got to be in it to win it", and which other game gives you the chance of winning a few million pounds for a £1.00 stake. In my view the best way to play the lottery is to forget about winning the jackpot but play a strategy to reduce the odds against winning the smaller prizes that way you get an increased chance of winning something and still have chance of getting the jackpot, or one of the larger prizes. Don't forget whatever selection of numbers you stake your wager on each set has the same chance of winning the jackpot.
So now you want to know how to increase those odds. Browse to the next page and I will tell you how.

If you have any comments or would like to contact me click on the bottle